A graphical interactive approach to multi-response optimization

Case study of a multi-response optimization problem where we outline our solution approach

José Núñez Ares

May 26, 2020 2 min read

Problem statement

In the article of Myers and Montgomery (1995)¹, the authors discuss an experiment with three factors:

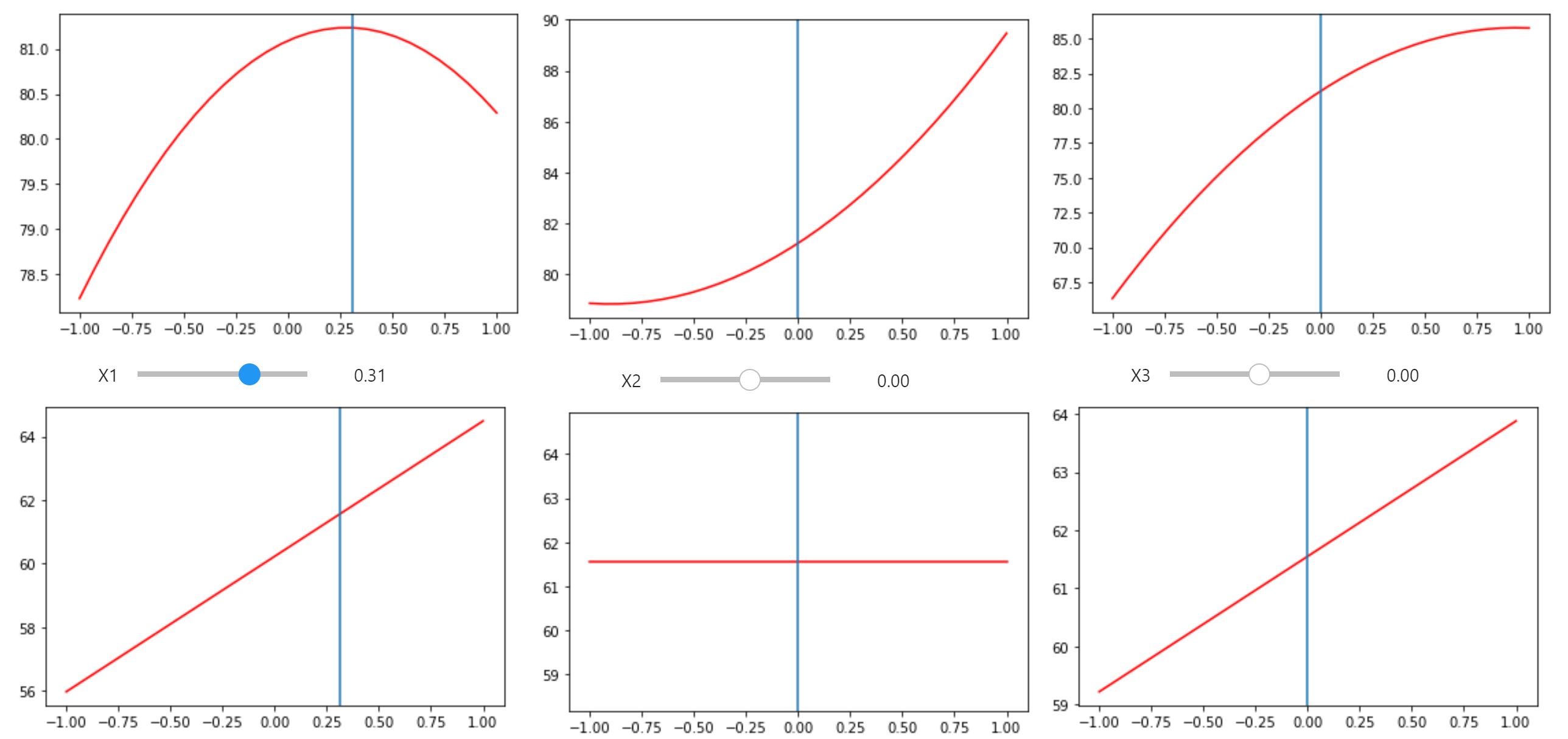
$x_1$: reaction time
$x_2$: reaction temperature
$x_3$: amount of catalyst

and two responses:

$y_1$: conversion of a polymer
$y_2$: thermal activity

The engineers seek to find the settings that maximize $y_1$ and achieve a target value of 57.5 for $y_2$.

Design

In Table we can see the experimental design used (a Central Composite Design with circumscribed axial points):

	$x_1$	$x_2$	$x_3$	$y_1$	$y_2$
1	-1	-1	-1	74	53,2
2	1	-1	-1	51	62,9
3	-1	1	-1	88	53,4
4	1	1	-1	70	62,6
5	-1	-1	1	71	57,3
6	1	-1	1	90	67,9
7	-1	1	1	66	59,8
8	1	1	1	97	67,8
9	-1,682	0	0	76	59,1
10	1,682	0	0	79	65,9
11	0	-1,682	0	85	60
12	0	1,682	0	97	60,7
13	0	0	-1,682	55	57,4
14	0	0	1,682	81	63,2
15	0	0	0	81	59,2
16	0	0	0	75	60,4
17	0	0	0	76	59,1
18	0	0	0	83	60,6
19	0	0	0	80	60,8
20	0	0	0	91	58,9

Models

The linear model for the first response is a full second-order effects model on the three factors:

$ y_1 =81.09+1.03x_1+4.64x_2+6.20x_3-1.86x_1^2+2.94x_2^2 $

$\phantom{y_1=}-5.19x_3^2+2.13x_1x_2+11.37x_1x_3-3.87x_2x_3$

The linear model for the second response includes only an intercept and two linear effects.

$ y_2 =60.23+4.26x_1+2.23x_3 $

Research question

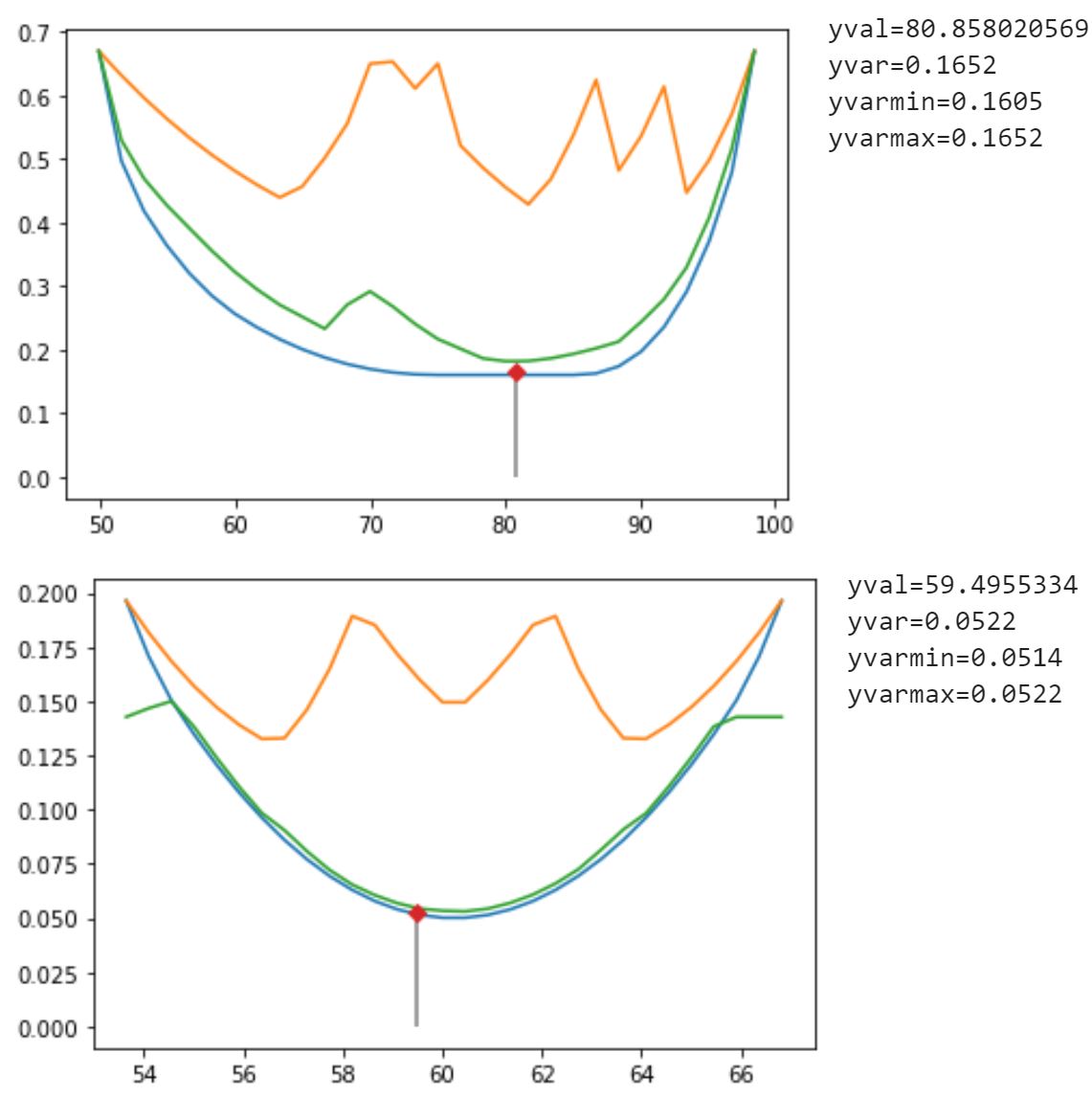
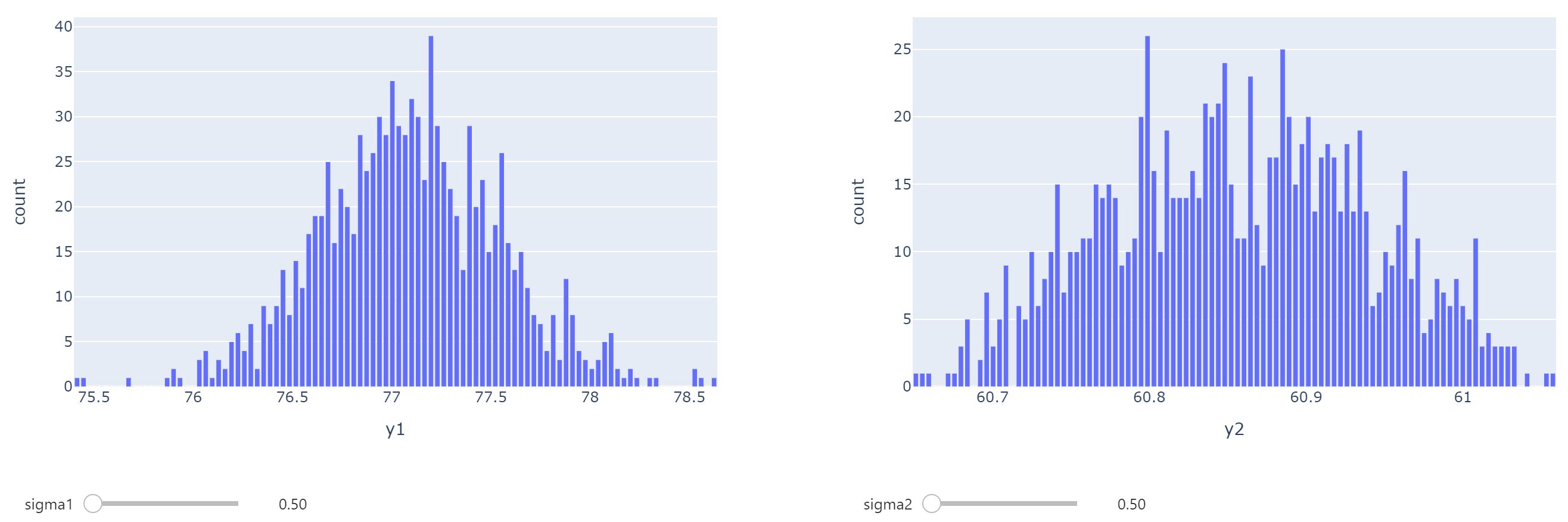
Can we optimize both responses simultaneously while taking into account the prediction variance and the robustness of the solution against variability in the factor levels and model coefficients?

We refer to the book of Goos and Jones²: for theoretical background on these issues

Draft of our solution approach

We present a highly interactive solution approach, which consists of 5 interconnected graphs.

Prediction profiler
Variance profiler
Robustness against variation in the model coefficients

G. Geoffrey Vining (1998) A Compromise Approach to Multiresponse Optimization, Journal of Quality Technology, 30:4, 309-313, DOI: 10.1080/00224065.1998.11979867 ↩︎
Goos, Peter, and Bradley Jones. Optimal design of experiments: a case study approach. John Wiley & Sons, 2011. ↩︎

optimization parallel coordinates plot